Na metrologia, quando realizamos uma calibração, devemos nos preocupar com o número de medições realizadas.
O número de medições que realizamos em uma calibração diz muito sobre a confiabilidade dos resultados, desta forma fazer apenas uma medição é ariscado do ponto de vista estatístico.
Na maioria das medições a melhor maneira disponível para estimar o valor esperado de uma grandeza, que varia aleatoriamente, e que n observações independentes obtidas sob as mesmas condições de medição é a média aritmética destas n medições.
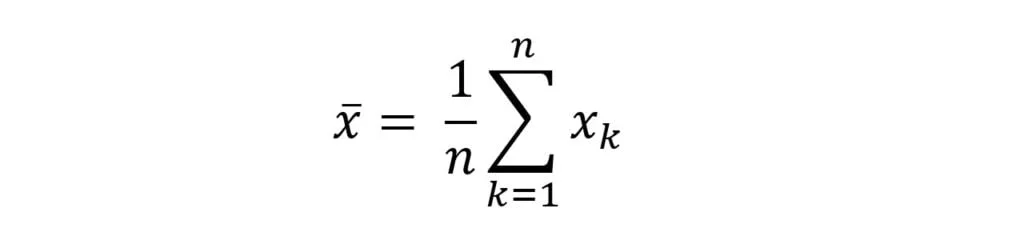
Realizar apenas uma medição pode gerar dúvidas sobre o valor que estamos medindo. Mesmo fazendo duas medições, se forem discordantes continuaremos em dúvida.
Porém devido a limitações financeiras ou de tempo, normalmente não realizamos uma grande quantidade de medições durante uma calibração.
Para usamos poucas medições durante a calibração, o conhecimento sobre o instrumento ou a grandeza medida é fundamental.
Em algumas calibrações há pouca variabilidade durante as medições desta forma não é necessária uma amostra grande.
Se fizemos no mínimo três medições, duas concordarem e uma for discordante, suspeitaremos apenas de um destes valores.
Desta forma para nos resguardamos de erros grosseiros durante uma calibração devemos no mínimo fazer três medições.
As influências durante a medição
Quando realizamos uma calibração temos cinco fatores que sempre vão influenciar nossas medições, podemos chamá-los de os 5Ms.

Todos estes fatores influenciam diretamente em nossas medições, por isso a importância de se conhecer bem o que estamos medindo.
Assim vai ficando cada vez mais claro que medir uma única vez é muito arriscado.
Avaliação do Tipo A da incerteza padrão e o número de medições
Segundo o VIM, a avaliação do Tipo A da incerteza de medição é a avaliação duma componente da incerteza de medição por uma análise estatística dos valores medidos, obtidos sob condições definidas de medição.
A incerteza do tipo A é parte estatística da incerteza de medição. Ela pode ser aplicada quando realizamos várias observações independentes nas mesmas condições de medição.
Se houver uma resolução suficiente no processo de medição, haverá uma dispersão observável ou propagação nos valores obtidos.
Na NIT-DICLA-021, no item referente a incerteza Avaliação do Tipo A da incerteza padrão, nos apresenta dois métodos para o cálculo desta componente.
Método 1
Uma estimativa da variância da distribuição de probabilidade fundamental é a variância experimental, que consiste em calcular o desvio padrão das leituras em seguida, dividimos o resultado pela raiz do número de leituras para obtermos a variância experimental da média.
Um exemplo prático para visualizarmos, imagine os alunos da 5ª série de uma escola, se calcularmos as alturas de todos estes alunos separados por sala de aula e calcularmos a média e o desvio padrão (valores em metros).
| SALA | 5ª A | 5ª B | 5ª C | 5ª D | 5ª E |
| ALTURA MÉDIA | 1,38 | 1,35 | 1,49 | 1,30 | 1,40 |
| DESVIO PADRÃO | 0,13 | 0,13 | 0,14 | 0,16 | 0,21 |
Considerando as médias obtidas em cada quinta série, calculando a média e o desvio padrão das salas, temos para a média 1,38 m e desvio padrão das médias é 0,07 m.
Podemos observar que dentro de uma determinada amostra temos uma variação, mas do ponto de vista populacional a média das medias das alturas é um valor considerado normal.
Este é o papel da variância experimental da média, a partir do desvio padrão de uma amostra ele estima o desvio padrão de uma certa população.
Método 2
Para uma medida bem caracterizada e sob controle estatístico, pode haver uma estimativa combinada ou agrupada da variância sp2 que caracteriza a dispersão melhor do que o desvio padrão estimado obtido a partir de um número limitado de observações.
Este método leva em conta a experiência e o conhecimento sobre a medição que estamos realizando.
Basicamente, a diferença entre os dois métodos é que no método 1 utilizamos quando o desvio padrão é calculado através dos dados obtidos na calibração em questão, normalmente com menos de dez medições.
Por exemplo na calibração de um micrômetro você obtém 03 leituras: 24,999 mm; 2,500 mm; 2,501 mm. O desvio padrão 0,001 mm é utilizado para calcular o desvio padrão experimental da média.
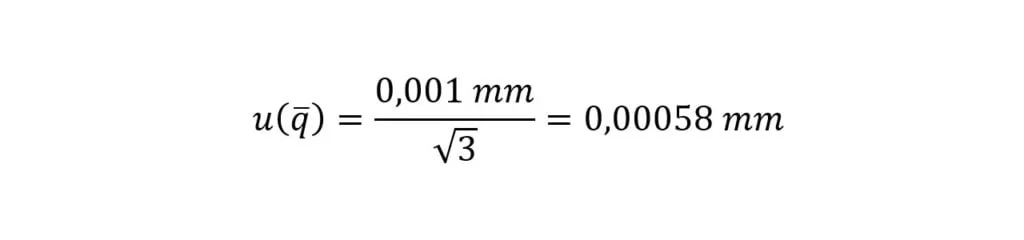
O método 2 é utilizado quando você tem calculado um desvio padrão histórico, normalmente maior do que 10 medições.
Por exemplo, o desvio padrão experimental agrupado que caracteriza a comparação entre dois blocos padrão, foi determinado como sendo 13 nm, determinado a partir de 25 observações repetidas e independentes.
Desta forma temos um valor histórico já conhecido. Se na calibração de blocos padrão realizarmos 5 medições, a incerteza associada com a média aritmética destas medições é:
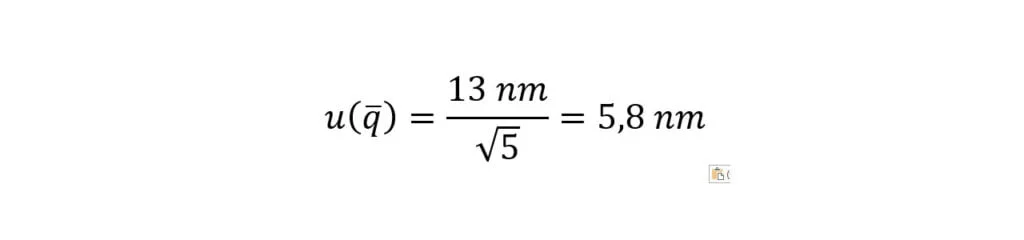
A NIT-DICLA-021, bem como a normatização vigente não obriga a utilizar um ou outro método, mas como já observamos , o conhecimento e a experiência é muito importante quando realizamos uma medição.
Caso o número de medições não puder ser aumentado, outros meios de avaliação da incerteza devem ser considerados, como a histerese entre as medições, por exemplo, pois sem conhecimento suficiente sobre uma calibração, acredito que seja melhor pecar por excesso do que por falta de componentes.
Número de medições e o fator de abrangência k
Estimar os graus de liberdade efetivos veff da incerteza padrão a partir da fórmula de Welch-Satterhwaite.
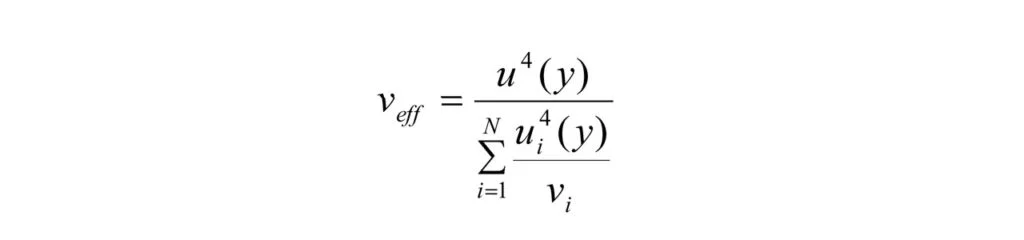
Esta fórmula serve para calcular a confiabilidade da incerteza padrão associada ao resultado da medição:
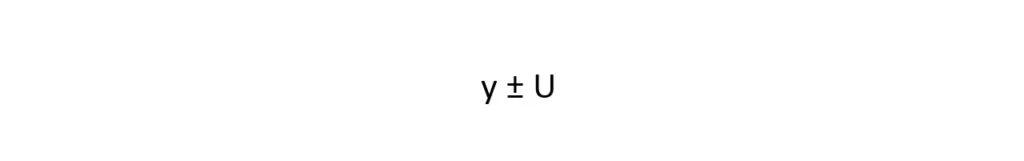
Onde y é o valor da grandeza medida e U a incerteza expandida associada.
Normalmente quando o Veff calculado apresenta valores menores que 50, deixa o k maior que dois.
Isso pode ocorrer devido ao baixo número de medições ou as componentes de incerteza estabelecidas não são suficientes para estimar a incerteza da medição realizada.
| Veff | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 20 | 50 | ∞ |
| k | 13,97 | 4,53 | 3,31 | 2,87 | 2,65 | 2,37 | 2,28 | 2,13 | 2,05 | 2,00 |
Fatores de abrangência k para diferentes graus de liberdade Veff
Quando medimos uma única vez não temos graus de liberdade, se medimos 2 vezes temos um grau de liberdade e assim por diante, desta forma, se a variação entre as medições é muito grande influência diretamente cálculo do fator de abrangência k, pois quanto mais variações entre as medições menor é o grau de confiança, sobre o resultado da medição.
Por isso a importância de um número coerente de medições ou observações durante a calibração.
O objetivo deste artigo é mostrar a importância de realizamos mais de uma medição para aumentar a confiabilidade nossas calibrações.
Portanto, busque todas as informações possíveis do que você está medido para que com esse conhecimento seja possível justificar o número de medições que está utilizando e com isso sempre buscar melhor qualidade e confiança em suas medições.
SEJA UM APOIADOR DO CANAL METROLOGIA E GANHE INCRÍVEIS RECOMPENSAS
Fontes
EA-4/02 Evaluation of the Uncertainty of Measurement In Calibration
NIT-DICLA-021: Expressão da incerteza de medição por laboratórios de calibração


