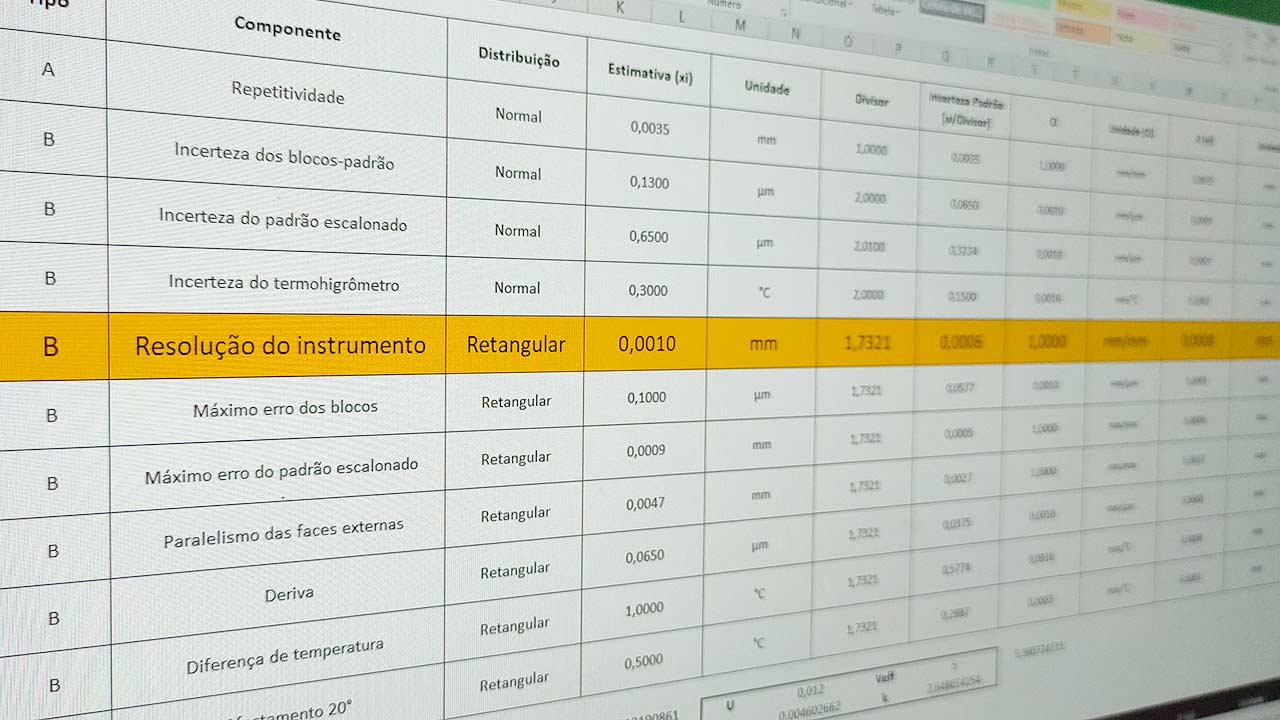
Na estimativa da incerteza de medição a contribuição da resolução de leitura de um instrumento de medição deve ser avaliada como uma incerteza tipo B, conforme estabelece o Guia da Expressão da Incerteza de Medição (ISO GUM).
É importante avaliar essa contribuição, pois não é nada incomum encontrarmos uma baixa dispersão dos valores obtidos de um processo de medição, o que caracteriza uma incerteza tipo A próxima a zero.
Nestes casos, dependendo do valor da resolução e do tipo de distribuição de probabilidade adotados, esta poderá ser uma das maiores, ou a maior, contribuição na incerteza final.
Resolução de leitura
Vamos, inicialmente, definir o que é resolução de leitura.
Segundo o Vocabulário Internacional de Metrologia (VIM), resolução de leitura é:
“a menor diferença entre indicações mostradas que pode ser significativamente percebida”.
VIM, 2012
Não devemos confundir a resolução de leitura com a menor divisão da escala do instrumento de medição.
A avaliação da resolução é feita em função do tipo de instrumento. Nos medidores com mostradores digitais a resolução corresponde ao incremento digital, ou seja, a menor divisão de leitura.
Já nos instrumentos com mostradores analógicos, a resolução, teoricamente, poderia ser “zero”.
No entanto, em função das limitações do operador, da qualidade do dispositivo indicador e da própria necessidade de leituras mais ou menos criteriosas, a resolução adotada poderá variar.
Para uma escolha adequada da resolução de leitura não podemos ignorar a sensibilidade do instrumento, ou seja, “quociente entre a variação de uma indicação de um sistema de medição e a variação correspondente do valor da grandeza medida”.
A resolução nunca será menor que a sensibilidade.
Distribuição retangular
Uma distribuição uniforme, ou retangular, é definida para um intervalo de valores finitos. Sua forma gráfica pode ser observada na Figura a seguir:
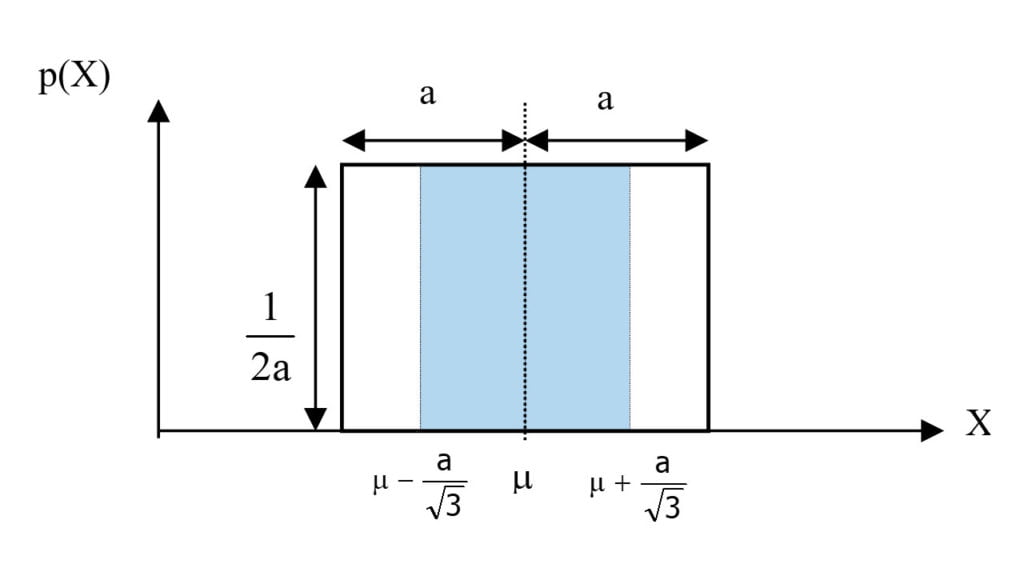
O desvio padrão da distribuição retangular é dado pela seguinte equação: [latex]s=\frac { a }{ \sqrt { 3 } } \quad[/latex]
Na metrologia a distribuição retangular é adotada, na maioria dos casos, para a resolução de leitura dos instrumentos de medição por ser uma distribuição mais conservativa, ou seja, aumenta um pouco mais a incerteza final.
Na dúvida de qual distribuição adotar recomenda-se usar a distribuição retangular, já que ela não privilegia nenhum intervalo e fornece uma maior incerteza.
Distribuição triangular
Quando a distribuição de probabilidade é maior na parte central, num intervalo definido, e decair linearmente nas extremidades, estaremos diante de uma distribuição triangular, conforme observado na figura a seguir.
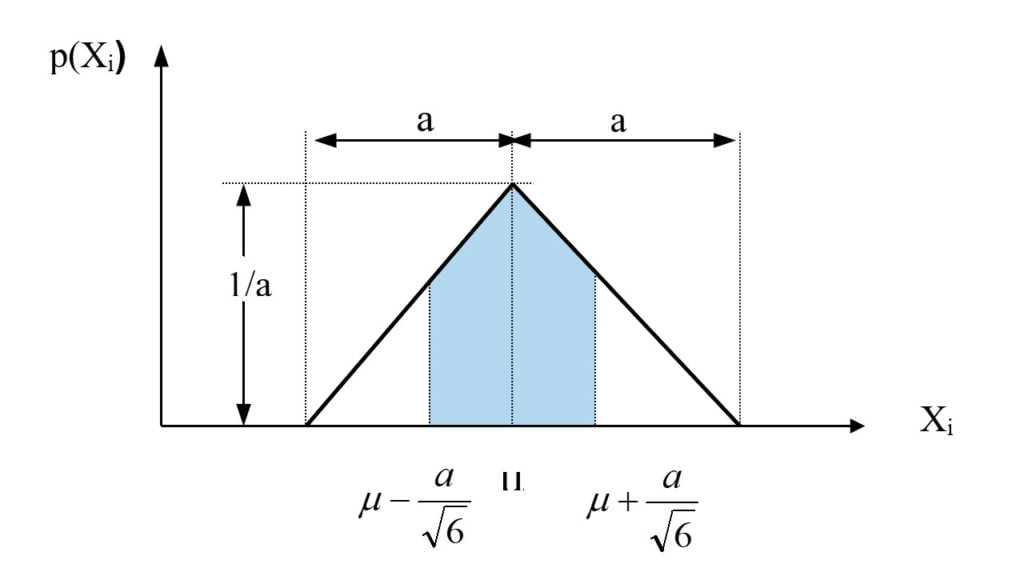
O desvio padrão da distribuição triangular é dado pela seguinte equação: [latex]s=\frac { a }{ \sqrt { 6 } } \quad[/latex]
Alguns profissionais de metrologia adotam esta distribuição para a resolução de indicadores analógicos, e sua utilização faz com que a incerteza final seja menor do que se utilizarmos a retangular. Mas, de fato, quando devemos empregá-la?
Incerteza de medição
Vamos entender primeiro o que é incerteza de medição.
A incerteza de medição, conforme definido no VIM, é um:
parâmetro não negativo que caracteriza a dispersão dos valores atribuídos a um mensurando, com base nas informações utilizadas.
VIM, 2012
Este parâmetro pode ser, por exemplo, um desvio padrão (ou um múltiplo dele), ou a metade de um intervalo correspondente a um nível da confiança declarado.
Resultado de medição
O resultado de uma medição é somente uma aproximação, ou uma estimativa, do valor do mensurando.
Desta forma, a apresentação do resultado é completa somente quando acompanhado por uma quantidade que declare a sua incerteza.
Assim, o resultado da medição (RM) deve ser expresso na forma [latex]RM=\bar { X } \pm U[/latex] [unidade de medição], onde [latex]\bar { X }[/latex] é a média dos resultados obtidos do conjunto de medições e U é a incerteza final expandida.
Incerteza do resultado
A incerteza do resultado de uma medição é uma combinação de vários componentes e que podem ser agrupados em duas categorias de acordo com as características do método usado para estimar seus valores numéricos: são as incertezas tipo A e as incertezas tipo B.
As incertezas tipo A são as oriundas da variação do próprio processo de medição, e as incertezas tipo B são determinadas a partir de informações acessórias e externas ao processo de medição.
Essas informações podem ser obtidas de resultados de medições similares anteriores, experiência ou conhecimento do comportamento do instrumento, dados do fabricante, dados fornecidos por certificados de calibração, referências de manuais de instrução etc.
São exemplos deste tipo de incerteza:
- Afastamento da temperatura ambiente em relação à temperatura de referência estipulada;
- Resolução de leitura (analógica ou digital);
- Incerteza do padrão;
- Instabilidade do padrão;
- Deformações mecânicas;
- Erro de histerese;
- Instabilidade temporal etc.
Uma vez que apresentamos resolução de leitura, incerteza e incerteza tipo B, passemos ao detalhamento de nossa análise de qual a melhor distribuição de probabilidade a ser adotada para a resolução.
Numa medição nos deparamos com duas situações:
1: Medição onde “buscamos” o valor da grandeza desejada
Ou seja, não sabemos a priori qual o valor a ser encontrado.
Esta situação é encontrada, por exemplo, na calibração de termômetros (onde o valor do ponto é fixado no banho térmico e lê-se o sinal gerado pelo termopar, pelo termorresistor ou a indicação no termômetro de líquido em vidro – TLV), de paquímetros e micrômetros (o valor do ponto de calibração é o do bloco padrão), e de balanças (o valor do ponto é o da massa padrão).
Exemplificando

Suponha que o valor da massa de um objeto seja 25,9 g e que a balança digital utilizada para essa medição tenha uma divisão de leitura de 0,1 g, ou seja, a resolução de leitura é de 0,1 g.
Se considerarmos que o algoritmo existente na balança digital (responsável pela digitalização dos valores das leituras) garante que o último dígito está no intervalo de [1 + ½] dígito, o “valor verdadeiro” da massa estará compreendido entre o intervalo [25,85 g a 25,95 g].
Valor de 25,96 g será arredondado pelo instrumento para 26,0 g, da mesma forma que 25,84 g para 25,8 g.
Logo, toda vez que a balança indicar 25,9 g teremos uma dúvida do “verdadeiro valor” da massa em questão, ocasionada pela sua limitação de resolução.
Considerando que a probabilidade do “valor verdadeiro” estar compreendido entre [25,85 g a 25,95 g] é a mesma dentro deste intervalo, o correto é adotar uma distribuição estatística que reflita este comportamento, ou seja, a distribuição retangular ou uniforme.
A incerteza da resolução, então, será igual o desvio padrão da distribuição retangular com a = 0,05 g (½ da resolução), ou seja, [latex]s=\frac { 0,05 }{ \sqrt { 3 } } =0,03\quad g\quad[/latex].
2: Medição onde “fixamos” o valor desejado
Esta situação é encontrada, por exemplo, na calibração de manômetros quando utilizamos uma bomba comparativa (o valor do ponto é fixado no objeto e a leitura realizada no manômetro padrão) e na calibração de multímetros (aplica-se o sinal – tensão, corrente ou resistência – no instrumento e realiza-se a leitura no multímetro padrão).
Quando fixamos o valor desejado, sabemos, a priori, o valor mais provável do mensurando, desta forma, faz sentido atribuir uma probabilidade maior a este valor.
Assim, devemos considerar que a distribuição triangular é a que melhor representa a distribuição de probabilidade da resolução de leitura do instrumento.
Exemplificando

Suponha que na calibração de um manômetro industrial, de faixa de medição (0 a 50) bar e resolução 1 bar, ao utilizarmos uma bomba comparadora fixamos os pontos de calibração no manômetro objeto em 10 bar, 20 bar, 30 bar, 40 bar e 50 bar.
Como esses valores foram fixados prioritariamente apresentarão uma probabilidade de ocorrência maior do que qualquer outro.
Como a resolução do manômetro é 1 bar, significa dizer que o menor valor lido no instrumento é 1 bar.
Assim, o “valor verdadeiro” da pressão, por exemplo no ponto 30 bar, estará compreendido no intervalo de [29,5 bar a 30,5 bar].
Valor de 30,6 bar será arredondado para 31 bar, da mesma forma que 29,4 bar para 29 bar.
Logo, toda vez que na calibração o manômetro objeto indicar 30 bar, haverá uma dúvida do “verdadeiro valor” da pressão em questão, ocasionada pela sua limitação de resolução.
Considerando que a probabilidade do “valor verdadeiro” estar compreendido entre [29,5 bar a 30,5 bar] é maior no ponto 30 bar do que em qualquer outro valor, porque fixamos neste valor, o correto é adotar uma distribuição estatística que reflita este comportamento: a distribuição triangular.
A incerteza da resolução, então, será igual ao desvio padrão da distribuição triangular com a = 0,5 bar (½ da resolução), ou seja, [latex]s=\frac { 0,5 }{ \sqrt { 6 } } \quad bar=0,2\quad bar\quad[/latex].
Conclusão
Não devemos associar a distribuição de probabilidade da resolução em função do instrumento ser analógico ou digital, e sim em função da probabilidade da medição ser uniforme ou triangular.
A tabela a seguir resume as considerações sobre o tipo de distribuição a ser adotado para a resolução de leitura, tanto para o padrão quanto para o instrumento a ser calibrado.
| Padrão | Instrumento | Fixar o ponto de leitura | Distribuição (Instrumento) | Distribuição (Padrão) |
| Digital | Digital | Independe | Retangular | Retangular |
| Digital | Analógico | Padrão | Retangular | Retangular |
| Analógico | Digital ou analógico | Padrão | Retangular | Triangular |
| Digital ou analógico | Analógico | Instrumento | Triangular | Retangular |
Fonte
Livro Metrologia e Incerteza de Medição: conceitos e aplicações | Alexandre Mendes e Pedro Paulo Novellino do Rosário.
Vocabulário Internacional de Metrologia (VIM 2012)